NO.1-10¶
001：两数之和¶
题目¶
题目截图如下：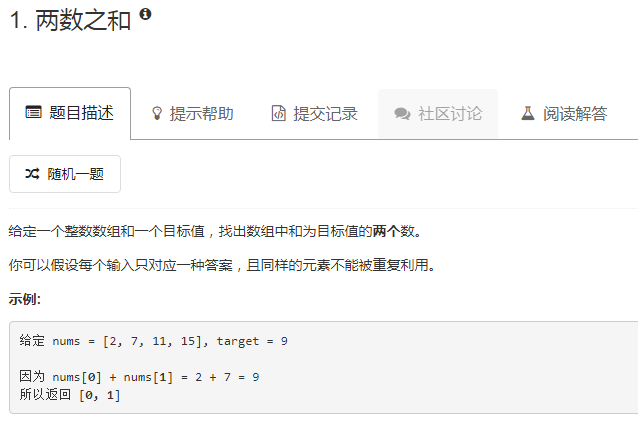 
我的版本一¶
class Solution:
def twoSum(self, nums, target):
for i1,v1 in enumerate(nums):
for i2,v2 in enumerate(nums):
if i1 == i2:
continue
if v1+v2 == target:
return [i1,i2]
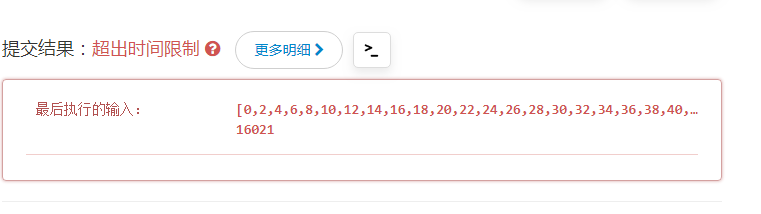
用两个for循环，理解起来没难度。基本小白都会想到的。在自测数据下，由于数据量小，与其他解法的差异并不明显。但是，在LeetCode
20个测试数据里，就会显示超时了。果然，简单的思路，易理解，但是耗费时间和性能。
我的版本二¶
class Solution:
def twoSum(self, nums, target):
for index,value in enumerate(nums):
answer = target - value
if answer in nums:
result_index = nums.index(answer)
if result_index == index:
continue
return [index, result_index]
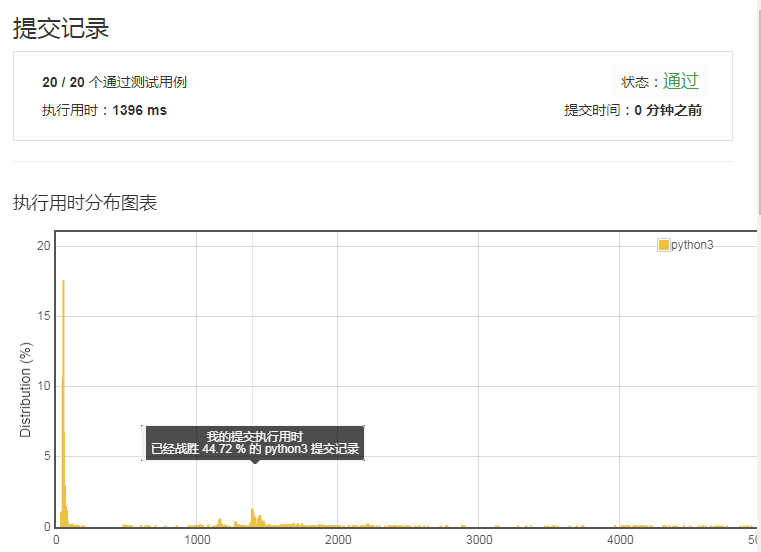只击败了44%的人，还是不行。还是得再优化，于是就尝试在网上搜寻一下其他解法。
大神的版本¶
class Solution:
def twoSum(self, nums, target):
dic = dict()
for index,value in enumerate(nums):
sub = target - value
if sub in dic:
return [dic[sub],index]
else:
dic[value] = index
还有这种
class Solution(object):
def twoSum(self, nums, target):
arr = {};
length = len(nums);
for i in range(length):
if (target - nums[i]) in arr:
return [arr[target - nums[i]], i];
arr[nums[i]] = i;
仔细看了下代码，代码相对逻辑复杂，你还会发现这段代码有bug，不过官方给的测试数据不够完善，没有检测出来。
由于dict的key，是不能重复的，所以当有两个值是相等的时候，由于索引被后面的值覆盖，就会导致返回的值不准确。
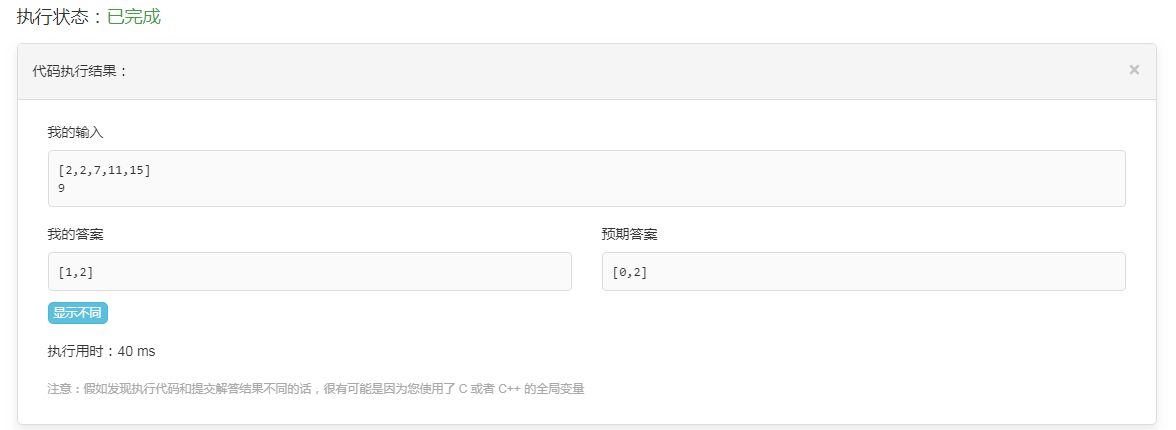
比如，我输入的值列表是[2,2,7,11,15]，由这个程序算出来的是[1,2]，而LeetCode预期答案是[0,2]，不通过。
这里也提醒大家，对网上的代码，一定要多加思考，提高自己阅读代码的能力。
但是，以上代码也是有可取之处的。因为字典的查询速度是非常快的。如果数据量大的话，请一定第一时间想到字典。
最终优化版¶
针对这个情况，我对以上代码进行各取所长，整理优化。
class Solution:
def twoSum(self, nums, target):
my_dict = {}
for index, value in enumerate(nums):
if (target - value) in my_dict:
return [my_dict[target - value], index]
if not my_dict.get(value):
my_dict[value] = index
执行一下，震惊了我的小伙伴。竟然打败了97.79%的人。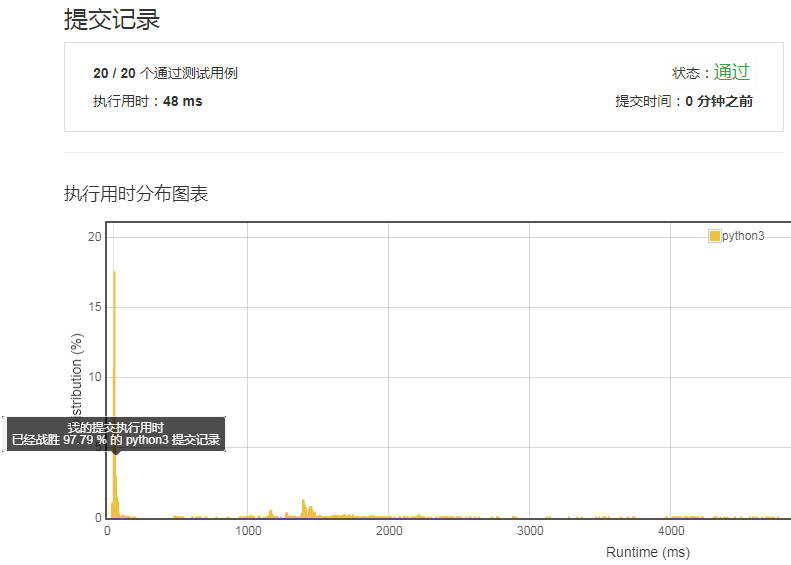 
002：两数相加¶
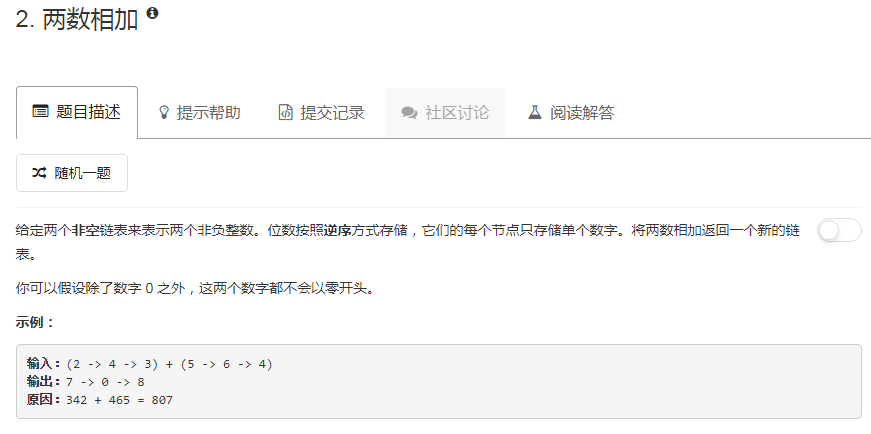
题目¶
准备知识¶
第一眼看到这个题目，小明真的懵逼了。不怕大家笑话，小明不是CS科班出身，没有尝过数据结构和算法这些个基础课程。关于我的个人背景，在「」里有提到，感兴趣的同学，可以看一下。
但是小明并不怕，现学现用，一直是小明很喜欢干的事。不能总是准备好了再出发，等你花尽心机用了几个月时间去学完了数据结构和算法，却早已精疲力尽，忘记了初衷。
为了完成这道题，我立马上网，搜寻了数据链表 的相关知识。
我的版本一¶
class Solution(object):
def addTwoNumbers(self, l1, l2):
"""
:type l1: ListNode
:type l2: ListNode
:rtype: ListNode
"""
head = _head = ListNode(0)
flag = 0
while l1 or l2:
v1 = v2 = None
if l1:
v1 = l1.val
l1 = l1.next
if l2:
v2 = l2.val
l2 = l2.next
v1 = v1 or 0
v2 = v2 or 0
flag, value = divmod(v1+v2+flag, 10)
_head.next = _head = ListNode(value)
if not l1 and not l2 and flag == 1:
_head.next = _head = ListNode(1)
del v1,v2
return head.next
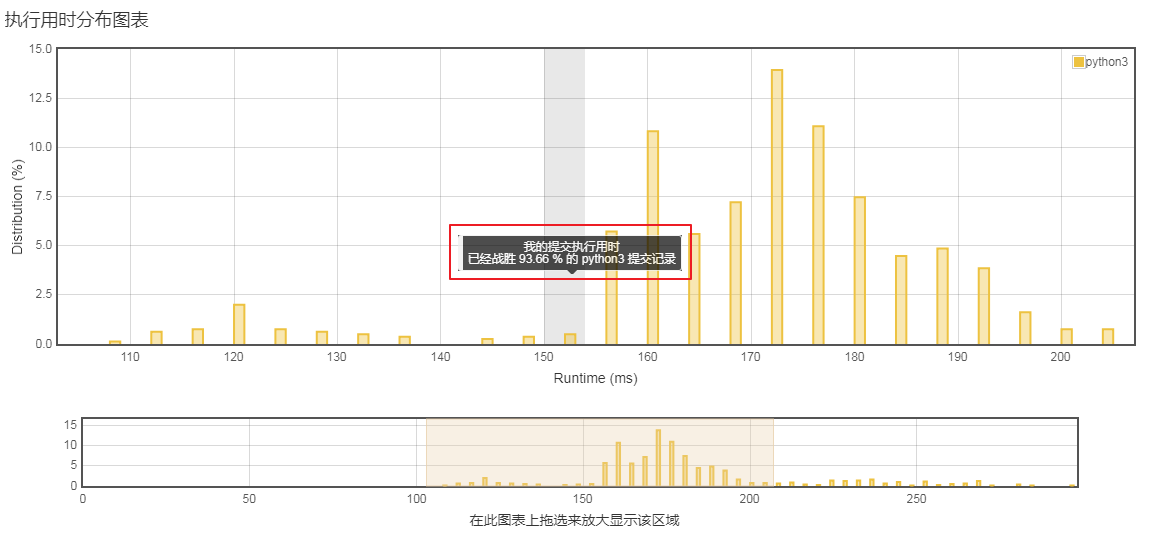
运行一下，还算理想。击败了93.66%，今天又可以加个鸡腿了。
大神的版本¶
按照惯例，还是上网去看看别人的优秀代码。结果，真的让小明大吃一惊，和我一样的逻辑，但是代码可对我精练多了。大家可以对比学习一下。
class Solution(object):
def addTwoNumbers(self, l1, l2):
"""
:type l1: ListNode
:type l2: ListNode
:rtype: ListNode
"""
head = p = ListNode(0)
carry = 0
while l1 or l2 or carry:
if l1:
carry += l1.val
l1 = l1.next
if l2:
carry += l2.val
l2 = l2.next
carry, val = divmod(carry, 10)
p.next = p = ListNode(val)
return head.next
难点梳理¶
在以上代码中，有一个新手可能难以理解的是，下面这个用法。
class Node:
def __init__(self, val):
self.val = val
self.next = None
header = n = Node(2)
n.next = n = Node(4)
通常来说，Python 中的 = 很多人可能会理解为
赋值，在大多数情况，赋值确实很通俗易懂，但是在如上这种情况下，如果你再用
赋值 去理解，你可以发现，怎么都解释不通。
所以这里，小明认为，= 准确的理解 应该是 引用。
第一句 header = n = Node(2)
Node(2)首先在内存中取得一席之地（内存地址），存放其值。
然后，创建一个变量名为header的对象，并将其指向Node(2)的地址。
最后，再创建一个变量名为n的对象，也将其指向Node(2)的地址。
这样，header和n就都是Node(2)的代言人，对header和n中的任一变量做改变，另一变量也将随之变化，因为他们两个本就是一个对象。
>>> a = b = [1,2,3]
>>> a
[1, 2, 3]
>>> b
[1, 2, 3]
>>> # 对b添加元素
>>> b.append(6)
>>> b
[1, 2, 3, 6]
>>> a # 发现a也随之改变
[1, 2, 3, 6]
第二句 n.next = n = Node(4)
Node(4)首先在内存中取得一席之地（内存地址），存放其值。
然后，将之前的变量n的next属性，指向Node(4)的地址。本质上是改变了Node(2)的next
指向的是Node(4)
最后，将变量n重新指定Node(4),这时候，n就相当于header.next。
说起来有点绕。但请一定要理解这个引用的思想。
003：无重复字符的最长子串¶
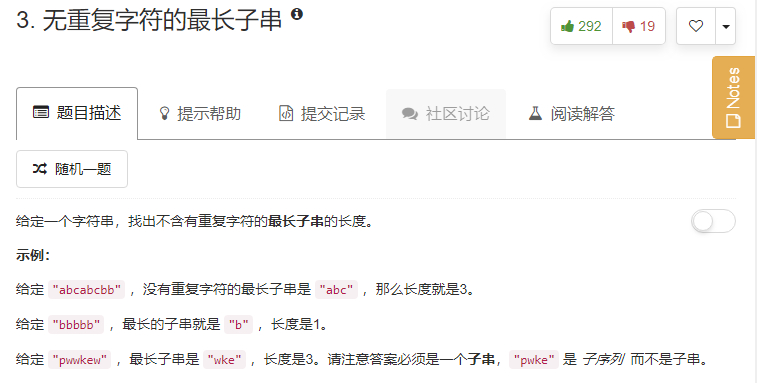
题目¶
审题¶
今天这道题，看起来是不是很简单？
但做为一道中等难度的题目，它可不会让你失望。敲起你的键盘，试着来解下这道题，你会很难找到一个好的思路。
事实上，想这个思路也确实花了我不少的时间，是写代码时间的好几倍。
首先，要理解 子串 和 子序列 的区别。
子串：必须同时具备，连续性和唯一性。 子序列：只须具备唯一性即可。
我的版本¶
先说下我的思路。
假设一个字符串的长度是10，那我就先从字符串的[0,1]子串查起，假如子串里没有重复字符（通过set()去重查看），就继续查看子串[0,2]，如果还是没有重复，就继续查看[0,3]，这时候，我们发现这个子串里有重复字符（比方说，子串”abcb”），接下来，我们就要找出是在重复的那个字符的索引（查出是b，在索引1处）。那下次我们查找的子串就不是[0,5]了，而是[2,5]，就这样一直往下，直到遍历完整个字符串。
class Solution:
def lengthOfLongestSubstring(self, s):
if len(s) == 1:
return 1
reset_start= False
start = 0
max_len = 0
for i in range(len(s)):
# reset_start就为True，需要重新设置起点
if reset_start:
start = new_start
# 为什么加1，是因为第一次start会和end一样是0
end = i + 1
sub_str = s[start:end]
len_sub_str= end - start
if len(set(sub_str)) != len_sub_str:
# 找出是在哪个位置重复
rep_index = sub_str.index(s[i])
new_start = rep_index + start + 1
reset_start= True
continue
if len_sub_str > max_len:
# 记录下迄今为止最在长度
max_len = len_sub_str
reset_start = False
return max_len
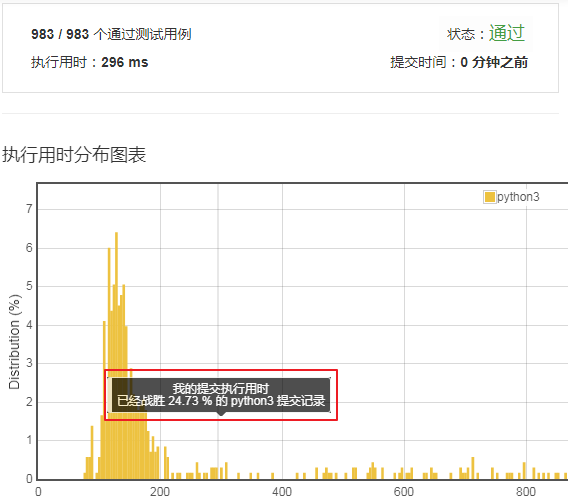
运行一下，结果很差。只击败了24.73%。今天吃不了鸡腿了。不过小明真的是尽力了。只能想到这个思路。
大神的版本¶
按照惯例，还是上网去看看别人的优秀代码。
真是惊叹，果然是思路决定出路啊。
这种解法很巧妙。
定义两个变量longest和left，longest用于存储最长子字符串的长度，left存储无重复子串左边的起始位置。
然后创建一个哈希表，遍历整个字符串，如果字符串没有在哈希表中出现，说明没有遇到过该字符，则此时计算最长无重复子串，当哈希表中的值小于left，说明left位置更新了，需要重新计算最长无重复子串。每次在哈希表中将当前字符串对应的赋值加1。
class Solution(object):
def lengthOfLongestSubstring(self, s):
longest = 0; left = 0; tmp = {}
for index, each in enumerate(s):
if each not in tmp or tmp[each] < left:
# 计算当前最长的长度
longest = max(longest, index - left + 1)
else:
left = tmp[each]
tmp[each] = index + 1
return longest
运行一下，看看吧，击败了92.3%。众望所归啊。 佩服佩服。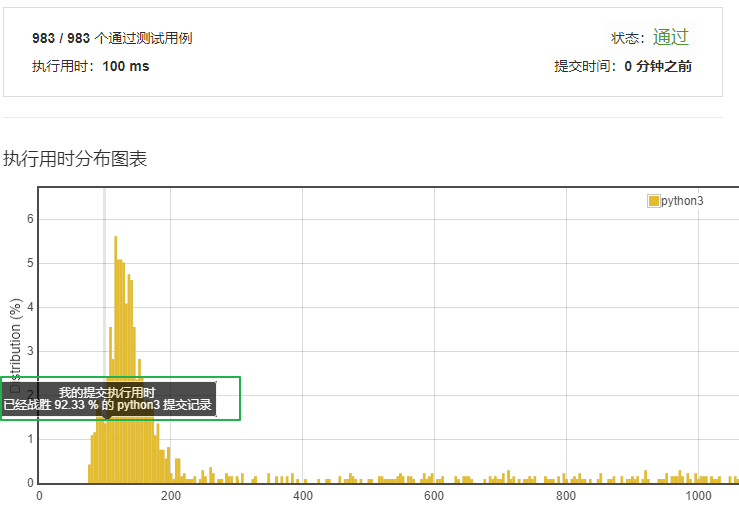 
总结¶
其实我的思路，和上面那个优秀代码的思路是一致的。
我做得不好的一点是，在检测当前子串是否重复这一点上面，我选了一个效率非常低的做法，就是每次循环都要计算下
len(set(str_obj)) 和
len(str_obj)，而这种是相当耗时的，而且会随着字符串长度的增长，耗时也线性增加。
而聪明的人，则是通过维护一个字典，来存放唯一值，和唯一值的最大索引。对执行速度的提升，可以说是非常显著的。
004：两个排序数组的中位数¶
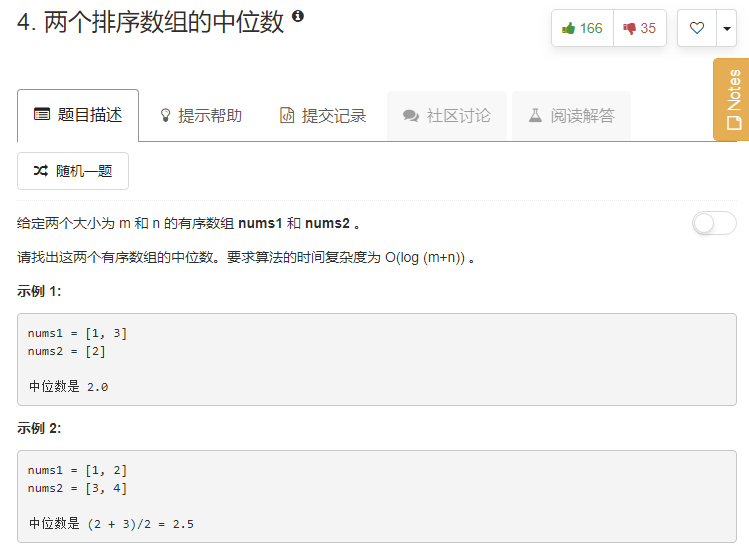
题目¶
背景知识¶
我发现leetcode上的题，都有一个特点，就是初一看，这么简单。再一看，真tm难。
我把这道题发群里，不少人觉得这道题简单。我只能说你去试着做一下就清楚了。
这道题，在难度系数为5，这是什么概念呢。是LeetCode是难度系数最高的。
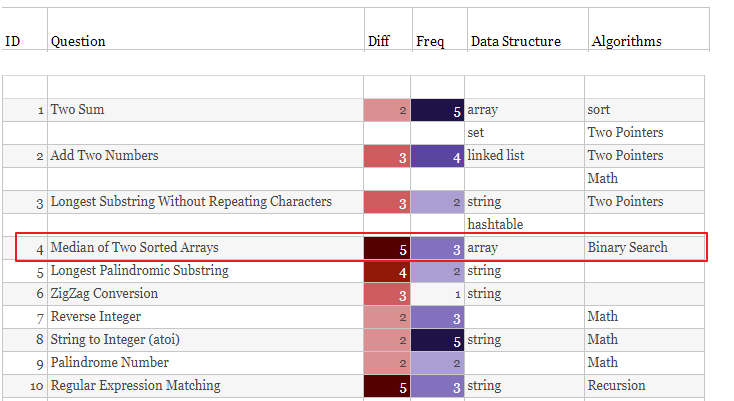
这道题，要想做对。
需要知道两个知识。 - 什么是中位数 - 什么是时间复杂度为O(log(n+m))
第一点，什么是中位数。 比方说： 奇位数：[3, 6, 9]的中位数是6
偶位数：[3, 6, 8, 9]的中位数是6+8/2 = 7
第二点：时间复杂度。 什么是时间复杂度，我也很难讲得明白。如果你需要了解更多，你可以去找本算法的书，亦或者网上搜下。我这里只能讲本节需要了解的知识噢。
log级别的时间复杂度，老司机都会联想到「二分查找法」。
咱们举个例子说，现在让你在一个有序列表 [1,3,6,7,9,13,15,17,23]
里找出17在哪个位置上。使用二分查找法，是先拿这个列表最中的数9，先和17进行比较，发现17>9，那再拿9后面的子列表[13,15,17,23]的最中间的数，由于是偶数，咱们取中位数16和17对比，发现小于16<17，再后面的子列表[17,23]的中位数20和17对比，发现17<20，最后只剩下17这一个数了，取出其索引，就知道他的位置了。
上面这个列表长度是9，用时间复杂度来看，就是
其意思是说，最多需要3次。和我们上面例子，找出17的位置用了三次（这是最坏的情况下用的次数）是吻合的。
一定要注意的是，使用二分查找法的前提是列表已经是有序。这和我们本道题，并不一样。
我的答案¶
惭愧。这道题三个小时我都没做出来，没有想到一个好的思路。遂放弃。
即使这样，在看别人的答案时，依然有一种醍醐灌顶的感觉（前提是你有思考过）。具体的解析，在下面我会来剖析，不然相信有不少人会看不懂。
网上的答案¶
ewe >对于一个长度为n的已排序数列a。 若n为奇数，中位数为a[n / 2 + 1], 若n为偶数，则中位数(a[n / 2] + a[n / 2 + 1]) / 2; 如果我们可以在两个数列中求出第K小的元素，便可以解决该问题; 不妨设数列A元素个数为n，数列B元素个数为m，各自升序排序，求第k小元素; 取A[k / 2] B[k / 2] 比较; 如果 A[k / 2] > B[k / 2] 那么，所求的元素必然不在B的前k / 2个元素中(证明反证法); 反之，必然不在A的前k / 2个元素中，于是我们可以将A或B数列的前k / 2元素删去，求剩下两个数列的; k - k / 2小元素，于是得到了数据规模变小的同类问题，递归解决; 如果 k / 2 大于某数列个数，所求元素必然不在另一数列的前k / 2个元素中，同上操作就好。
如果人读上面的思路觉得难以理解，让小明来试着解释一番。
如果是奇数，那么中位数必定在两个列表A和B中的某个元素。 如果是偶数，那么中位数一定是两个元素的平均数。
那么问题，我们可以将其转化一下。
如果是奇数，就要再两个列表里找到一个第m小的数。
如果是偶数，就要再两个列表里找到一个第n小和第n+1小的数，然后再取平均数。
现在思路比较清晰了，无论是哪种情况，我们都得找到第k小的数。所以我们得实现一个这样的公共函数。
整个问题的精髓都在这个公共函数里。包括上面的二分查找法的思想，也将在这里面体现。
class Solution(object):
def findMedianSortedArrays(self, nums1, nums2):
"""
:type nums1: List[int]
:type nums2: List[int]
:rtype: float
"""
len1, len2 = len(nums1), len(nums2)
if (len1 + len2) % 2 == 1:
# 是奇数
return self.getKth(nums1, nums2, (len1 + len2)//2 + 1)
else:
# 是偶数
return (self.getKth(nums1, nums2, (len1 + len2)//2) +
self.getKth(nums1, nums2, (len1 + len2)//2 + 1)) * 0.5
# 公共函数：查找两个列表里第k小的数
def getKth(self, A, B, k):
m, n = len(A), len(B)
# 保证A比B长度短
if m > n:
return self.getKth(B, A, k)
left, right = 0, m
# 这个while循环，是找A中<=(整个有序数组中第k个数)的最大数
while left < right:
mid = left + (right - left) // 2
# --------------------------------------------
# x = k - 1 - mid：表示在B中前k-mid个的索引
if 0 <= k - 1 - mid < n and A[mid] >= B[k - 1 - mid]:
# 进入这里，表明B中的前k-mid个都比中位数小，被剔除
right = mid
else:
# 进入这里，表明A中的前mid个都比中位数小，被剔除
left = mid + 1
# --------------------------------------------
Ai_minus_1 = A[left - 1] if left - 1 >= 0 else float("-inf")
# 这个是找B中<=(整个有序数组中第k个数)的最大数
Bj = B[(k - left) - 1] if k - 1 - left >= 0 else float("-inf")
return max(Ai_minus_1, Bj)
在看代码的时候，上面两长线包围的代码块，是最难以理解的部分，这里再解释一下。
假设我们要找两个列表里第k小的数，那么必将有x个在A列表，k-x个在B列表。 如何找出这个x是何值呢，就使用二分查找法，一次一次试探。
先从A列表中找到最中间的数（这边使用//，向下取整，假设其索引为m），去和B列表中的第k-m，对比，如果A[m]<B[k-m]，那么说明A的前m个元素都比第k小的那个数小，可以剔除了。
接下来，到A[m+1:]的最中间的数（假设其索引为n）和B[:]中每(k-m)-n对比，和上面一样，再剔除一半，直到最后，只剩下一个数。这个数在A中比第k小的数小的最大数。听起来很绕，请一定去仔细阅读代码。
好啦。剖析就到这里。小明已经尽可能把这个解法讲得简单明了。相信比网上大多数的讲解都更加让人容易理解。
005：最长回文子串¶
题目¶
我的答案¶
先说一下，我的思路。
通过思考可知，可以使用中心扩展的方法，把给定的每一个字母当做中心，向两边扩展，这样找到最长的子回文串。算法复杂度为O(N^2)。 分为两种情况：
A类型：如aba，这样长度为奇数的回文
B类型：如abba，这样长度为偶数的回文
而无论是哪种情况，我们都得求出这个回环字符串的「起始索引」「终止索引」用于提取字符串，和「字符串长度」用于比较谁是最长的。这样我们就很明确了，我们需要这样一个公共函数（即
代码中的 calc_utils函数）。
class Solution(object):
def longestPalindrome(self, s):
len_str = len(s)
if len_str == 0:
return ""
max_sub_str=""
# 工具函数，若有回环字符串，则会进入此函数。
# 返回值回环字符串的「起始索引」「终止索引」「字符串长度」
def calc_utils(s, left, right, len_str, flag=False):
step = 0
while left-step >= 0 and right+step <= (len_str-1) and \
s[left-step] == s[right+step]:
step+=1
if flag==True:
step1 = step-1
return i-step1,i+2+step1,2*(step1+1)
else:
step2 = step
return i-step2,i+1+step2,2*step2+1
for i in range(len_str):
# 设置索引默认值
len1=len2=1
left1,right1 = i,i+1
left2,right2 = i,i+1
# 有A类型回环迹象
if i+1<len_str and s[i] == s[i+1]:
left1,right1,len1=calc_utils(s, i, i+1, len_str, True)
# 有B类型回环迹象
if i>0 and i+1 < len_str and s[i-1] == s[i+1]:
left2,right2,len2=calc_utils(s, i-1, i+1, len_str)
# 与历史最长回环对象对比，破记录了则记录
if max(len1,len2)>len(max_sub_str):
if len1>len2:
max_sub_str=s[left1:right1]
else:
max_sub_str=s[left2:right2]
return max_sub_str
感觉自己写得挺暴力的，来看看执行效率先。至少超过半数了，有52.12%，给自己加个鸡腿。
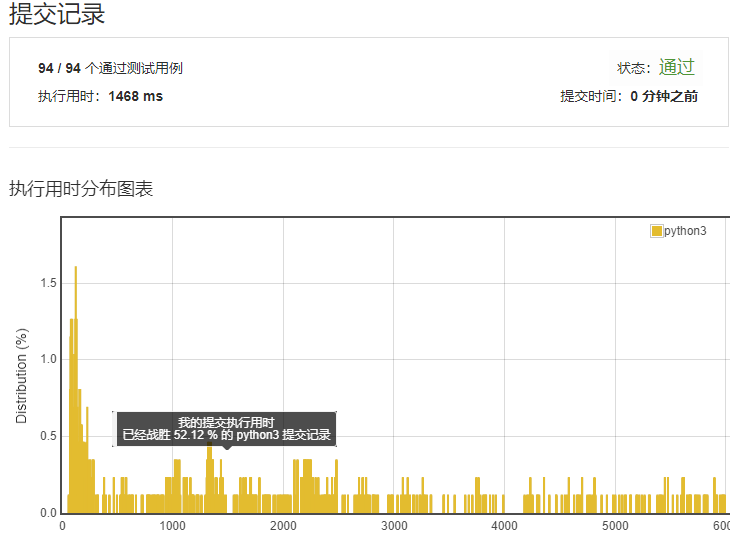
网上的版本¶
按照惯例，我们来学习下别人的优秀代码。
下面的代码，我看了很久才看懂。思想可以说是非常NB。
从上面的我的答案中，你可以看出，我需要以两种类型的回环字符串进行分类，然后进行计算。可以说是既繁琐又复杂。
那么有没有一种方法，可以让我们对这两种类型「一视同仁」呢，聪明的网友，给出了一种 让我叹为观止的算法:
「马拉车算法」 为了让大家知道，什么是马拉车算法？
我特地截了几张某博客的文章。给大家做参考。 
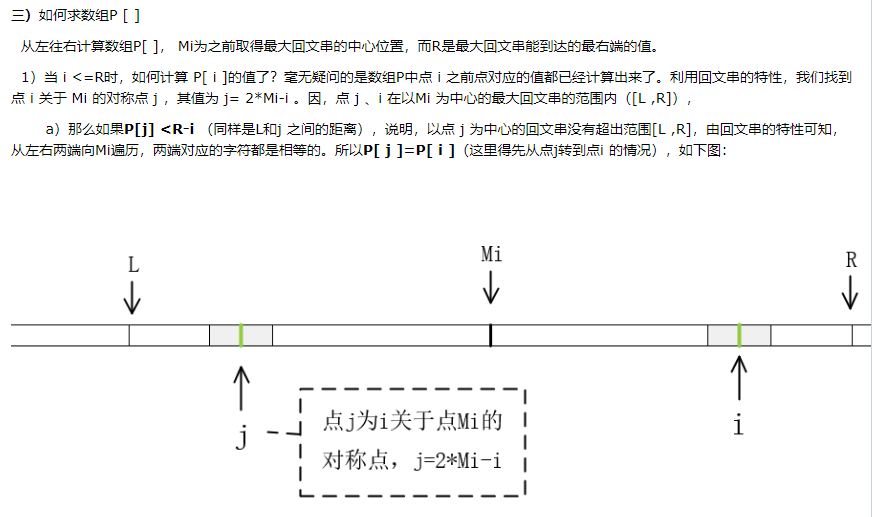
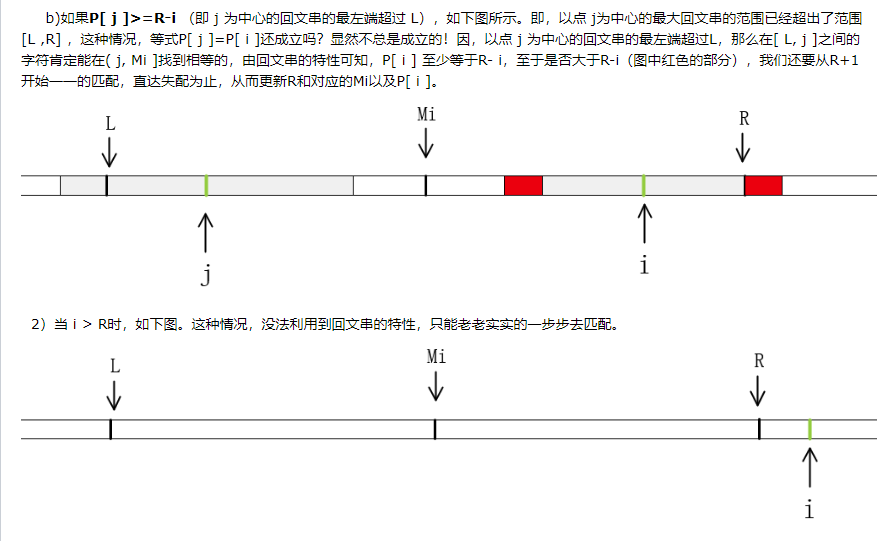
截自：https://www.cnblogs.com/love-yh/p/7072161.html
大家理解完上述思想后，再阅读或者调试如下代码，可能会更有收获。
class Solution(object):
def longestPalindrome(self, s):
def preProcess(s):
if not s:
return ['^', '$']
T = ['^']
for c in s:
T += ['#', c]
T += ['#', '$']
return T
T = preProcess(s)
P = [0] * len(T)
center, right = 0, 0
for i in range(1, len(T) - 1):
# P[i]是虚假的回环串长度
# i_mirror 是真实的回环串长度
i_mirror = 2 * center - i
# 记录上一循环的回环串长度
if right > i:
P[i] = min(right - i, P[i_mirror])
else:
P[i] = 0
# 查找以当前字母为中心的回环串，并记录P[i]=长度
while T[i + 1 + P[i]] == T[i - 1 - P[i]]:
P[i] += 1
# 避免..a#b.. 情况下中的#在P[i]中被记为1
if i + P[i] > right:
center, right = i, i + P[i]
max_i = 0
for i in range(1, len(T) - 1):
if P[i] > P[max_i]:
max_i = i
start = (max_i - 1 - P[max_i]) / 2
return s[start : start + P[max_i]]
